Making A Rocket League Bot

2021-01-03

For the last few years, I've been obsessed with Rocket League, a physics-based game where rocket-powered cars play soccer. Being physics-based means that this game has an immensely high skill ceiling, not unlike sports in the physical world: there is no such thing as auto-aim.

The interaction between players and the game physics allows for amazing plays:

Or positively terrible plays, if you're more like the average player:

Given the difficulty of the game, the built-in AI isn't very good. Most players can surpass it within a few weeks of playing and must turn to online matches against other humans for an actual challenge.

I've always wondered how one might build a better bot for Rocket League. So when I discovered RLBot, a framework and community dedicated to making bots for Rocket League, I was thrilled. Finally, an interesting side project!

The Goal

Playing Rocket League well is a high bar. It involves predicting the motion of the ball and other players, planning your moves and executing them, positioning, strategizing, and more. For now, I'll settle for a much more modest achievement: scoring a goal. More specifically, I would like to build a bot that can hit the ball towards the net, regardless of the ball or car's starting state.

Solving this for certain starting states does seem relatively trivial. For example, if the car is facing the ball and the ball is between the car and the goal already, the car may just need to make a slight turn before driving straight at the ball.

But solving this in the general case is more challenging. Consider this case, where the ball is soaring through the air while the car is on the ground near a wall:

Scoring in this situation requires a complex string of maneuvers:

1. Turning to the right while on the ground
2. Transitioning up the curve of the wall
3. Driving straight on the wall at an angle
4. Jumping off at the appropriate moment
5. Boosting for height and speed
6. Flipping diagonally for additional horizontal velocity in the air
7. Boosting while angling the car to fine-tune the hit

Other situations require their own unique set of moves to hit the ball in the desired direction efficiently. But given an arbitrary scenario, where the car and ball may be anywhere on the field and going at any speed, how can we figure out the right set of moves that will accomplish our goal?

You Can Turn Anything Into A Graph

Rocket League's physics engine runs at 120fps. You could imagine that players make 120 decisions per second and provide appropriate controller inputs at each point. For practicality's sake, you might choose fewer/larger discrete steps. Regardless, we end up with a string of decisions and corresponding controller inputs, which result in a series of car states.

This string of inputs and states looks awfully like a tree. The car can make several different moves at each branching point. These moves result in new car states, and each resulting car state is a starting point for further branching:

The nodes of the tree are car states, and the edges between them are car inputs. This tree of inputs leads to all states that the car can reach, and so a tree search should find a path to a desirable state. Our desired endpoint is a car state that collides with the ball in such a way that the ball's post-collision velocity points at the goal. A path through the tree of inputs that reaches that state is our solution.

Note that there are many solutions in this tree since multiple paths can result in a goal. Here are two different solutions for the same position, and there are many more:

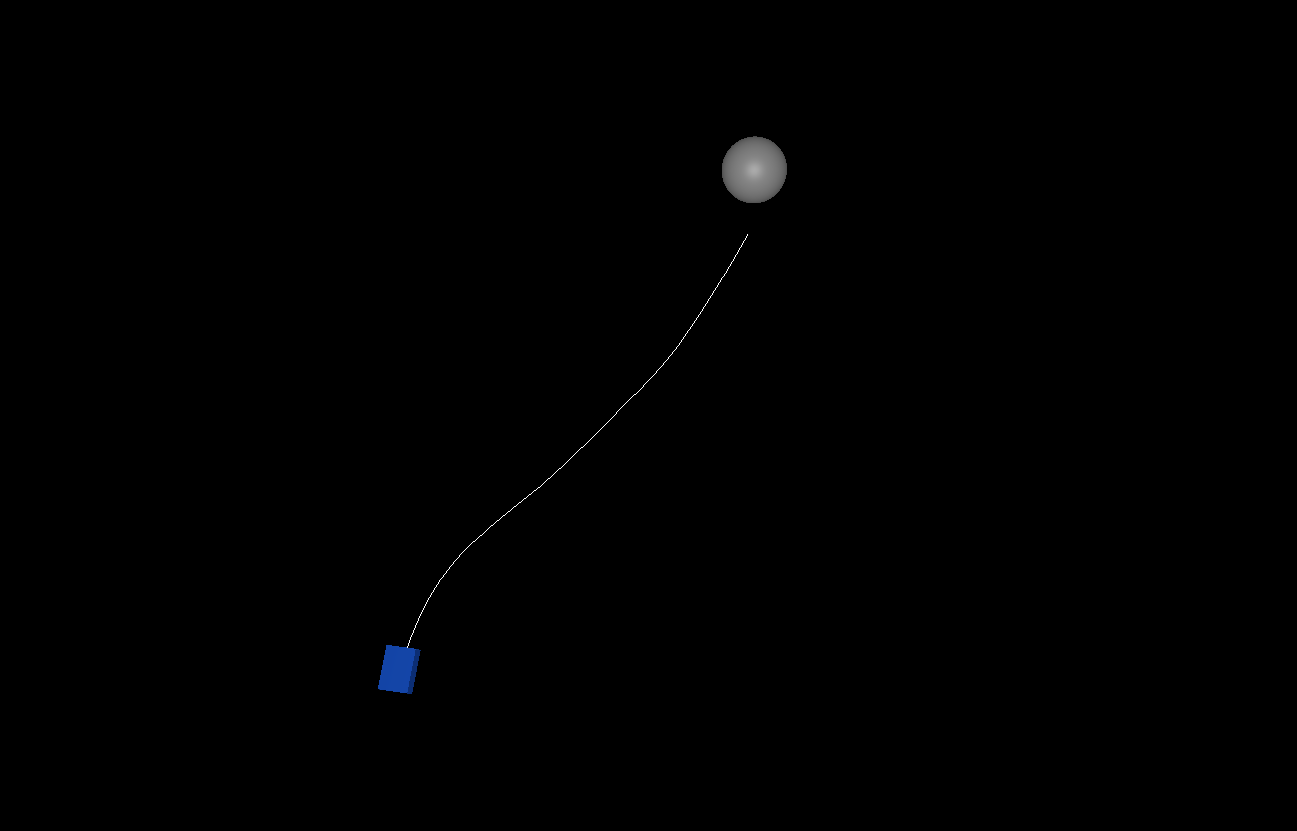
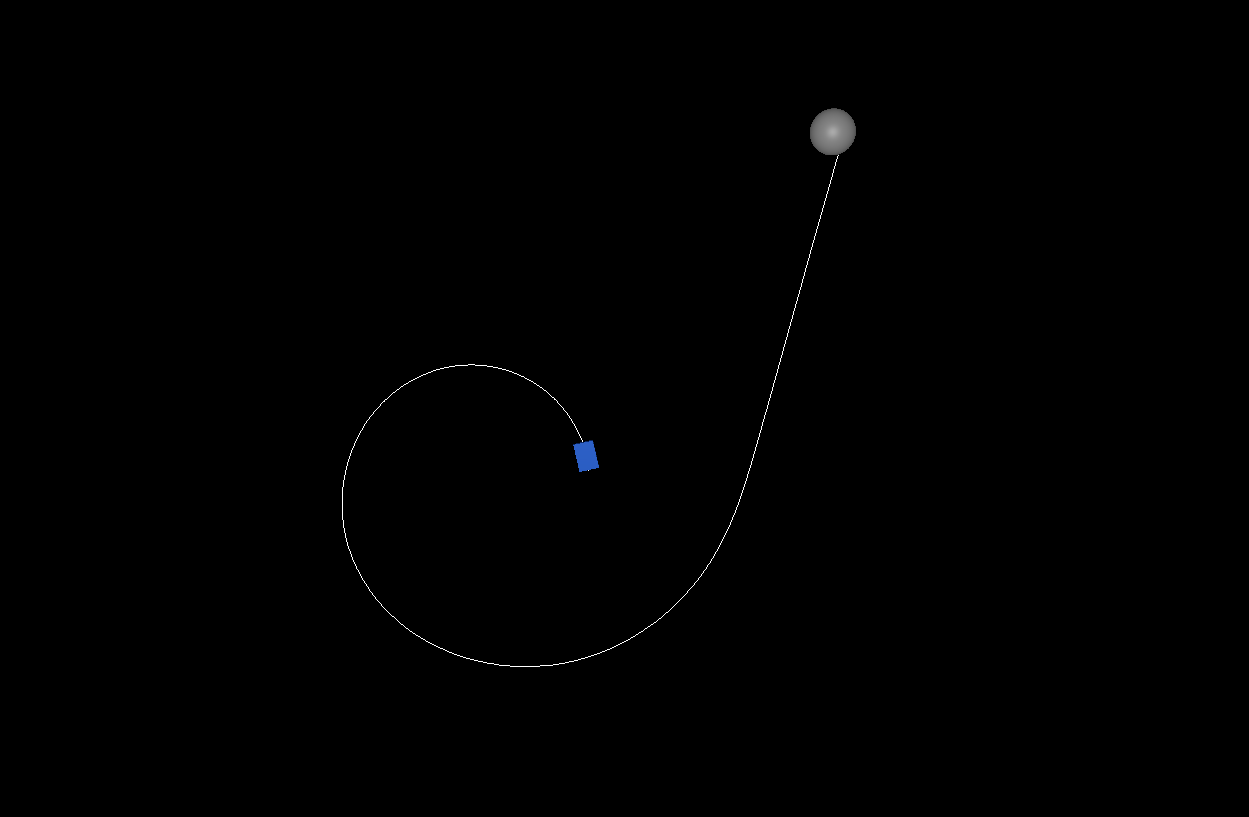
We don't want any old solution; we want the "optimal" solution. I.e., the solution that hits the ball as early as possible. In reality, there are situations in Rocket League where it makes more sense to slow down and get a different type of shot. But most of the time, the player who is fastest to the ball wins it. So we'll use the time to reach the ball as an evaluation function for optimality.

A*

We can use a path search algorithm, like Djikstra's algorithm or A*, to find an optimal path through the input tree. Djikstra's algorithm relies only on the cost between nodes of the tree. For our purposes, the cost of a single edge will be the amount of time we spend on a single input step. The entire path's cost is the sum of the costs along the edges, which corresponds to the total time it takes to hit the ball.

A* is an extension of Djikstra's algorithm for shortest path search and can achieve higher performance than Djikstra's algorithm by using a heuristic to guide the search. This heuristic is an estimate of cost given a node in the tree. We'll later discuss what heuristic would be appropriate for Rocket League. Suffice it to say that a well-designed heuristic can significantly reduce the runtime of the search.

Hybrid A*

But there are some challenges to applying A* to this particular search problem. It's most common to use A* to search paths in graphs of highly interconnected nodes, e.g., on a 2d grid. When multiple routes reach the same node, the algorithm can directly compare different paths. The nodes are equivalent regardless of the way we get there.

In contrast, the state of a car in Rocket League is a set of floating-point numbers, comprising its 3-dimensional position, velocity, angular velocity, and rotation. Two different car states can be right beside each other in state space yet far apart in the graph. And though it's possible to reach similar car states via divergent paths, those states will still be slightly different. This difference means that each new state's cost will be unknown and treated as if never seen before. Introducing rounding or discretization to the values when simulating car state would solve this, but at the expense of unacceptable simulation errors.

That's where the "Hybrid" A* algorithm comes in. This algorithm was introduced in the paper by Sebastian Thrun et al. entitled "Practical Search Techniques in Path Planning for Autonomous Driving." The technique helped Standford Racing Team's robot, Junior, achieve a 2nd place ranking in the 2007 DARPA Urban Challenge for self-driving cars.

The core idea behind the algorithm is to discretize the graph's nodes while also saving the full kinematic state of the car at each node. The discretization makes graph search feasible: when a new path reaches a state similar to a state found earlier via a different path, we can directly compare them. Keeping the one with the lowest estimated total cost significantly prunes the graph of similar nodes. Yet, we keep the full car state at the node for the winning path and thus maintain an accurate simulation.

Discretization of the State and Input Space

While the discretization applied at each node in the Hybrid A* algorithm gets us closer to feasibility, it does come at a cost: optimality. A pruned node could lead to the most optimal path. However, the path the algorithm finds will still be near the globally optimal path, as each discarded node is very close to nodes we do keep. We can tune the discretization according to the bot's performance needs by tweaking the bucket sizes to be as small as possible while still meeting the performance goal.

Despite the relative reduction in explored state space, we need further discretization to make path search feasible since the state space is still enormous. Most paths take several seconds for a Rocket League car to traverse. With inputs at 120fps, that leads to several hundred levels in the tree. Using larger simulation steps between tree nodes can substantially reduce the number of car states calculated: another tweakable trade-off between performance and optimality.

Even more important than the number of levels in the tree is the branching factor. Rocket League uses floats for the throttle, steering, roll, pitch, and yaw inputs. We will have to discretize this large space of allowed inputs. If we only allow driving on the ground without drifting, the car could still boost, reverse, or idle. Suppose we omit all those possibilities and only consider cars throttling at 100% and going completely straight, left, or right. In that case, we finally reach a branching factor of 3. Adding boosting, a boolean input allowing for higher acceleration, results in a branching factor of 6. Drifting (another boolean) on top of that brings it to a branching factor of 12.

Those 12 different inputs are sufficient for most ground driving in Rocket League. While that's still a high branching factor, we can't reduce it further without giving up far too much in optimality: drifting and boosting are essential to efficiently moving in Rocket League. So we'll be forced to reduce the number of levels instead to accommodate this. The right heuristic function will also really help here!

Heuristic function

The heuristic function can make or break the A* algorithm, hybrid or otherwise. While it's always possible to find examples of graphs where even a perfect heuristic gets the same performance as with Djikstra's algorithm, for typical graphs, an appropriate heuristic can improve performance by multiple orders of magnitude by expanding far fewer nodes of the graph.

The only requirement for a heuristic for A* search is that it be admissible. That means it can underestimate the cost but should never overestimate it. However, the closer we can get to the actual cost, the better the heuristic is at eliminating graph expansions. So our target heuristic gives an answer that is as close to the actual cost as possible but no higher.

Designing a good heuristic function for Rocket League is somewhat challenging. One reason for this is that cars, in Rocket League and in general, have nonholonomic constraints on their movement. That is just a fancy way of saying that steering a car to make it move left or right is not independent of its forward or backward movement. A car with omnidirectional wheels would be holonomic in contrast.

In path search for holonomic systems, a simple distance-based heuristic can usually be used with success. That is not the case with nonholonomic systems since nearby points in state space may be far apart in graph space. But let's go ahead and use Euclidean distance as a heuristic and see how it does.

Here is a visualization of all node expansions for a few different cases, which we will use as benchmarks. The blue cuboid is the car, and the sphere is the ball. Each short white line is a state that the Hybrid A* path search simulated, and the solid line from the car to the ball is the final solution. I've run these tests with a branching factor of six, which allows for basic ground driving (left, right, and forward) with or without boost.

In case 1, the car is facing forwards towards the ball and goal but offset in the x-axis. We simulated between 50 to and 30,000 states per search typically, in 1ms to 10.0ms. Sometimes we have a hard time finding a solution and have a huge spike in the number of states expanded.

Case 2 has the car facing away from the goal and in between the ball and goal. It has to go a long way around, but our distance-based heuristic is not smart enough to understand this and wastes a lot of time exploring the wrong side of the ball. This results in about 2 million states simulated in about 4 seconds.

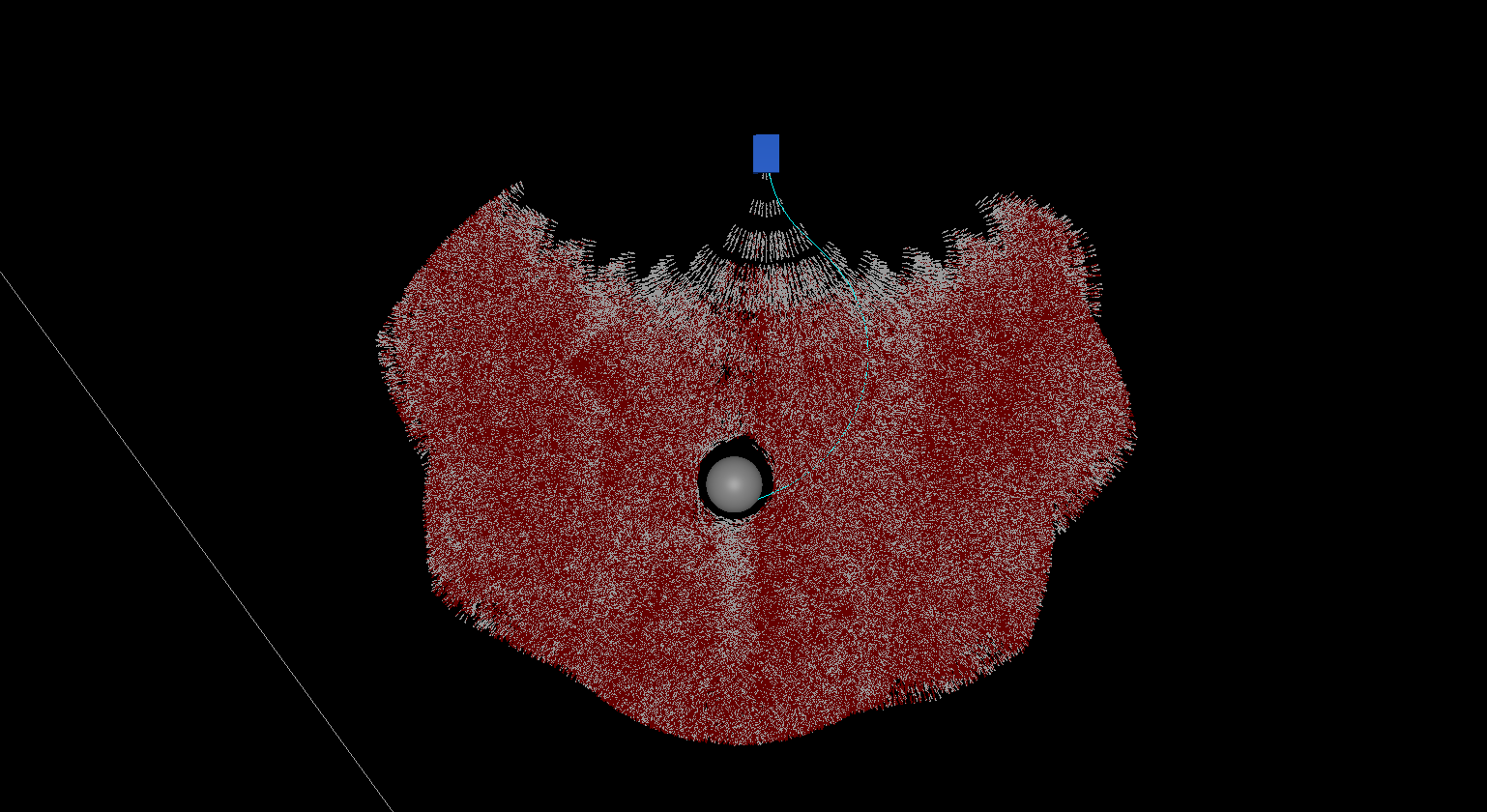
Case 3 is another challenging one, requiring a long roundabout turn to shoot the ball into the goal, and ends up simulating ~7m states, taking 11 seconds.

This abysmal performance clearly shows that a simple distance-based heuristic is not sufficient, especially in more challenging cases. The main reason for that is that a car cannot go directly sideways. So the distance heuristic sometimes thinks we are very close to reaching our goal, even though the car cannot turn so tightly.

Some have used Reeds-Shepp curves to get a better heuristic. This is a fast way to find a lower bound for distance.

While this is likely to work better than Euclidean distance, Rocket League's car driving physics are more complicated than the simple models used for Reeds-Shepp curves. For example, it is possible to drift at the expense of velocity, and the car's turning radius in Rocket League is dependent on its velocity. Furthermore, turning reduces a car's velocity.

More importantly, these curves only cover basic ground driving. It will not handle jumping, aerials (flying through the air with boost), transitioning from the ground to the wall, and various other moves we may want to accommodate in the general case.

I briefly attempted to use a simple 2-layer neural network as a heuristic function. Neural networks are known as universal function simulators, so it seemed like they could approximate the heuristic I wanted. I generated training and test data sets using optimal paths found by the algorithm with the Euclidean distance heuristic. We know the start state of the car for each found path and the actual cost for that state: the cost of that path.

Unfortunately, the results of this were mixed, and I've lost them now. I'm sure there is a way to make it work, e.g., I probably should have used polar coordinates instead of Euclidean ones as inputs to the neural network. But I moved on: while gathering data for the neural network, I had a better and much simpler idea.

You see, I now had a generated data set with car starting states in a grid across the entire field. I had different car orientations and velocities as well, plus the actual costs for each state. It looked something like this:

 cost,    x,    y, z, vx, vy, vz, etc
1.325, 1000, 1000, 0,  0,  0,  0, etc
  1.2,-1000,-1000, 0,  0,  0,  0, etc

I realized I could directly use this data instead of trying to compress it into a network! I just had to interpolate it based on how close my actual car state is to one of the states with a pre-computed cost.

Of course, I didn't invent that. It's a classic machine learning technique known as the k-nearest neighbors algorithm. A k-d tree can efficiently find states in the data set similar to a given one, e.g., one from the game. An average of these nearby states' costs, weighted by how close they are to the given state, can be used as a very accurate heuristic.

It seems that the overhead of the kNN algorithm outpaces the advantage of visiting fewer nodes in these cases.

Note that this averaging of actual costs will not result in an admissible heuristic. But admissibility is only a hard requirement for optimality, which we have already given up through all the discretization we did earlier in the process. If we're willing to give up more optimality for performance, we can even scale the heuristic function's cost. With a very accurate heuristic function such as the one we have, we still get a good result.

Here's the result of a 10x scaling factor on the kNN heuristic:

While some paths found this way are less than optimal, the runtime is much better. Also note that the solutions are all very similar to the globally optimal solution. That indicates that there should be a way to create a set of optimization passes that starts with the crude solution from a scaled heuristic and brings it closer to an optimal one, smoothing over some of the discretizations made while doing so. That's a future enhancement I'm interesting in pursuing.

What's Next

I've left out many details in this article required to make the Hybrid A* algorithm work for a Rocket League bot. I'd love to dive deeper into that. The visualizations here were all made using brick, my implementation of the ideas I explained in this article.

But brick still plays like, well, a brick. Errors can build up when applying a found plan to the actual game, which is a challenge to counteract. I have got a lot more I want to implement as well. For instance, I have not delved into driving on the wall and aerials. I'm also grappling with accurately simulating the drifting in Rocket League efficiently.

But all that will have to wait for next time!